CS224n-1

CS224N:Natural Language Processing with Deep Learning

Human language and word meaning

NLP的目标是设计算法让计算机理解自然语言，NLP的常见任务有：

难度	task
简单	Spell Checking 拼写检查
简单	Keyword Search 关键字搜索
简单	Finding Synonyms 寻找同义词
中等	Parsing	Parsing information from websites, documents, etc.
难	Machine Translation 机器翻译	e.g. Translate Chinese text to English
难	Semantic Analysis 语义分析	What is the meaning of query statement?
难	Coreference	e.g. What does “he” or “it” refer to given a document?
难	Question Answering	e.g. Answering Jeopardy questions

parse /pɑːz/
v. 对（句子）作语法分析；分析
n. （计算机）句法分析，句法分析结果

denotational semantics 指称语义学

指称语义学是一种用符号（word或者one-hot vector）表示含义的概念，这种表示是稀疏的，不能捕捉相似性。这是一种”localist” representation.

signifier(symbol) <—> signified(idea or thing)

WordNet

WordNet是一个包含同义词集（synonym sets）和上位词(hypernyms)(“is a” relationships)的列表的辞典

WordNet存在的问题：

1. WordNet是一个很好的资源，但忽略了同义词之间的细微差别
   • 例如“proficient”被列为“good”的同义词。这只在某些上下文中是正确的
2. 对words的新的含义无法及时更新：
   • 例如 wicked, badass, nifty, wizard, genius, ninja, bombest
   • 不可能永远保持更新words的新的含义
3. 主观
4. 需要人类劳动和调整
5. 无法计算单词之间的相似度

one-hot vector

one-hot vector: 用一个 $\mathbb{R}^{|V| \times 1}$ 向量表示每一个word，1位于这个word在词汇表中的索引位置，其余位置全是0。 $|V|$ 是词汇表的大小. 用这种形式编码的Word vectors 会以如下形式出现：

$$w^{a a r d v a r k}=\left[\begin{array}{c} 1 \\ 0 \\ 0 \\ \vdots \\ 0 \end{array}\right], w^a=\left[\begin{array}{c} 0 \\ 1 \\ 0 \\ \vdots \\ 0 \end{array}\right], w^{a t}=\left[\begin{array}{c} 0 \\ 0 \\ 1 \\ \vdots \\ 0 \end{array}\right], \cdots ,w^{z e b r a}=\left[\begin{array}{c} 0 \\ 0 \\ 0 \\ \vdots \\ 1 \end{array}\right]$$

one-hot vector存在的问题：

所有向量是正交的，没有相似性概念，并且向量维度过大。

Distributional semantics 分布语义学

这是基于word经常出现的上下文context表示一个word含义的概念。这种表示是密集的dense，可以更好地捕捉相似性similarity。

“You shall know a word by the company it keeps”(J. R Firth 1957: 11)
你可以通过一个单词的上下文了解它的含义 语言学家J. R Firth

分布语义学是现代统计NLP最成功的理念之一

当一个单词word出现在文本中时，它的上下文context是出现在其附近的一组单词(在一个固定大小的窗口中)

word vector, (word) embedding, (neural) word representations这三个概念等价，他们都是distributed representation，区别于”localist” representation

Word2vec

Efficient Estimation of Word Representations in Vector Space

Word2vec (Mikolov et al. 2013) 是一个学习word vectors的框架

• Word2vec
  • 我们有大量的文本 (corpus means ‘body’ in Latin. 复数为corpora)
  • 固定词汇表中的每个单词都由一个向量表示
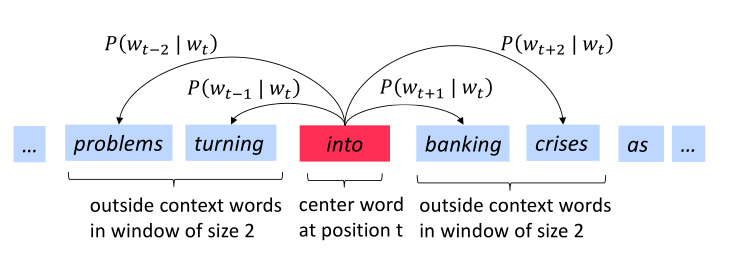
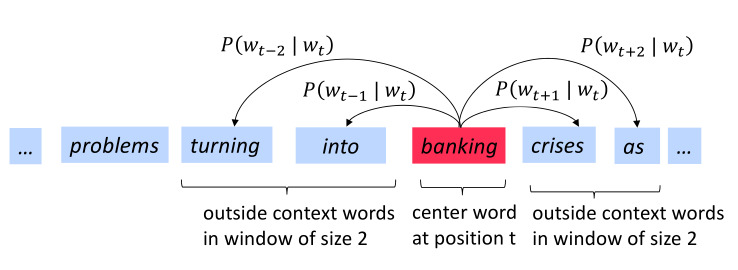
  • 文本中的每个位置t，其中有一个中心词c和上下文(“外部”)单词o
  • 使用c和o的词向量的相似性来计算给定c的o的概率 (反之亦然)
  • 不断调整词向量来最大化这个概率

下图为窗口大小为2时的$P\left(w_{t+j} \mid w_t\right)$计算过程，center word分别为into和banking

Word2vec: objective function(cost or loss function)

对于每个位置$t=1, \ldots, T$，在大小为m的固定窗口内预测上下文单词，给定中心词$w_t$，这个位置的似然为

$$\text {Likelihood}=L(\theta)=\prod_{\substack{t=1}}^T \prod_{\substack{-m \leq j \leq m \\ j \neq 0}} P\left(w_{t+j} \mid w_t ; \theta\right)$$

其中其中，$\theta$为所有需要优化的变量
损失函数$J(\theta)$是负的平均对数似然：

$$J(\theta)=-\frac{1}{T} \log L(\theta)=-\frac{1}{T} \sum_{t=1}^T \sum_{\substack{-m \leq j \leq m \\ j \neq 0}} \log P\left(w_{t+j} \mid w_t ; \theta\right)$$

最小化损失函数，等同于最大化预测精度

问题：如何计算$P\left(w_{t+j} \mid w_t ; \theta\right)$？
回答：对于每个word都是用两个向量
$v_w$，当w是一个centor word
$u_w$，当w是一个context word
c代表centor word，o代表context word

$$P(o \mid c)=\frac{\exp \left(u_o^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)}$$

Word2vec: prediction function

$$P(o \mid c)=\frac{\exp \left(u_o^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)}$$

取幂使任何数都为正
点积比较o和c的相似性 ，$u^T v=u·v=\sum_{i=1}^n u_i v_i$点积越大则概率越大
分母：对整个词汇表进行标准化，从而给出概率分布

这是一个softmax function：$\mathbb{R}^n \rightarrow(0,1)$的例子

$$\operatorname{softmax}\left(x_i\right)=\frac{\exp \left(x_i\right)}{\sum_{j=1}^n \exp \left(x_j\right)}=p_i$$

softmax将任意值$x_i$映射到概率分布$p_i$

首先我们随机初始化$u_w \in \mathbb{R}^d$和$v_w \in \mathbb{R}^d$，然后使用梯度下降法更新参数

$$\begin{aligned} \frac{\partial}{\partial v_c} \log P(o \mid c) & =\frac{\partial}{\partial v_c} \log \frac{\exp \left(u_o^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} \\ & =\frac{\partial}{\partial v_c}\left(\log \exp \left(u_o^T v_c\right)-\log \sum_{w \in V} \exp \left(u_w^T v_c\right)\right) \\ & =\frac{\partial}{\partial v_c}\left(u_o^T v_c-\log \sum_{w \in V} \exp \left(u_w^T v_c\right)\right) \\ & =u_o-\sum_{w \in V}\frac{\exp \left(u_w^T v_c\right) u_w}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} \end{aligned}$$

我们可以对上述结果重新排列如下，第一项是真正的上下文单词，第二项是预测的上下文单词。使用梯度下降法，模型的预测上下文将逐步接近真正的上下文。

$$\begin{aligned} \frac{\partial}{\partial v_c} \log P(o \mid c) & =u_o-\frac{\sum_{w \in V} \exp \left(u_w^T v_c\right) u_w}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} \\ & =u_o-\sum_{w \in V} \frac{\exp \left(u_w^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} u_w \\ & =u_o-\sum_{w \in V} P(w \mid c) u_w \end{aligned}$$

再对$uo$进行偏微分计算，注意这里的$u_o$是$u{w=o}$的简写，故可知

$$\frac{\partial}{\partial u_o} \sum_{w \in V} u_w^T v_c=\frac{\partial}{\partial u_o} u_o^T v_c=v_c$$ $$\begin{aligned} \frac{\partial}{\partial u_o} \log P(o \mid c) & =\frac{\partial}{\partial u_o} \log \frac{\exp \left(u_o^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} \\ & =\frac{\partial}{\partial u_o}\left(\log \exp \left(u_o^T v_c\right)-\log \sum_{w \in V} \exp \left(u_w^T v_c\right)\right) \\ & =\frac{\partial}{\partial u_o}\left(u_o^T v_c-\log \sum_{w \in V} \exp \left(u_w^T v_c\right)\right) \\ & =v_c-\frac{\sum \frac{\partial}{\partial u_o} \exp \left(u_w^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} \\ & =v_c-\frac{\exp \left(u_o^T v_c\right) v_c}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} \\ & =v_c-\frac{\exp \left(u_o^T v_c\right)}{\sum_{w \in V} \exp \left(u_w^T v_c\right)} v_c \\ & =v_c-P(o \mid c) v_c \\ & =(1-P(o \mid c)) v_c \end{aligned}$$

可以理解，当$P(o \mid c) \rightarrow 1$ ，即通过中心词c我们可以正确预测上下文词o，此时我们不需要调整$u_o$，反之则相应调整$u_o$。