线性代数（9）：正交投影与最小二乘法

参考资料:
清华大学数学科学系-线性代数-马辉
《工程数学 线性代数 第六版》 同济大学数学系 高等教育出版社
Linear Algebra by Gilbert Strang MIT麻省理工线性代数公开视频课

正交投影

回顾

首先复习下Ax=b在行空间中的唯一性，从几何直观上看，Ax=b在A的行空间中的唯一解，实际上是所有解在行空间里面的投影。

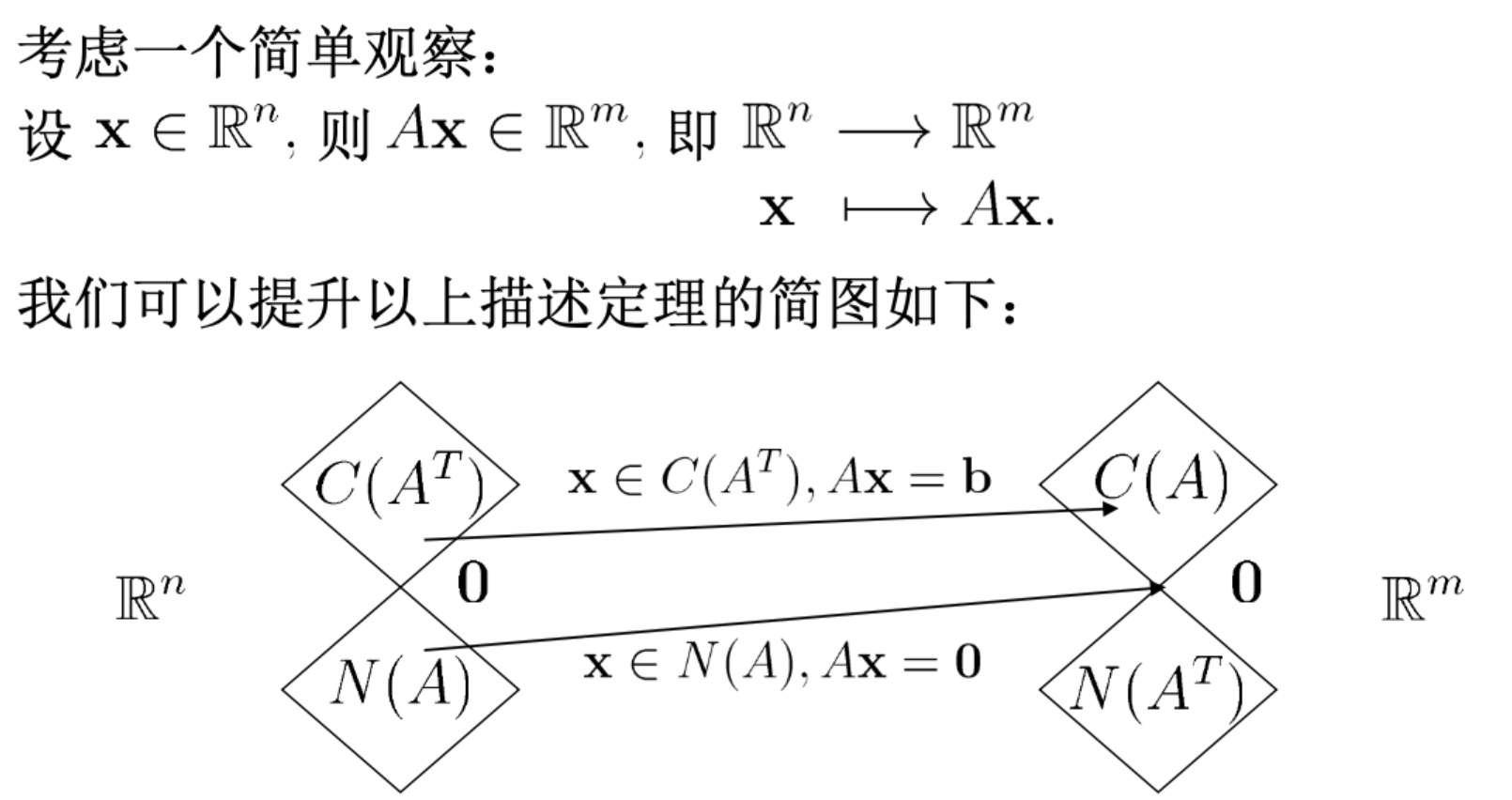
定理：若$A \mathbf{x}=\mathbf{b}$有解，则$A \mathbf{x}=\mathbf{b}$在$C\left(A^{T}\right)$中有唯一解

我们首先学习下投影的概念

点在直线上的投影

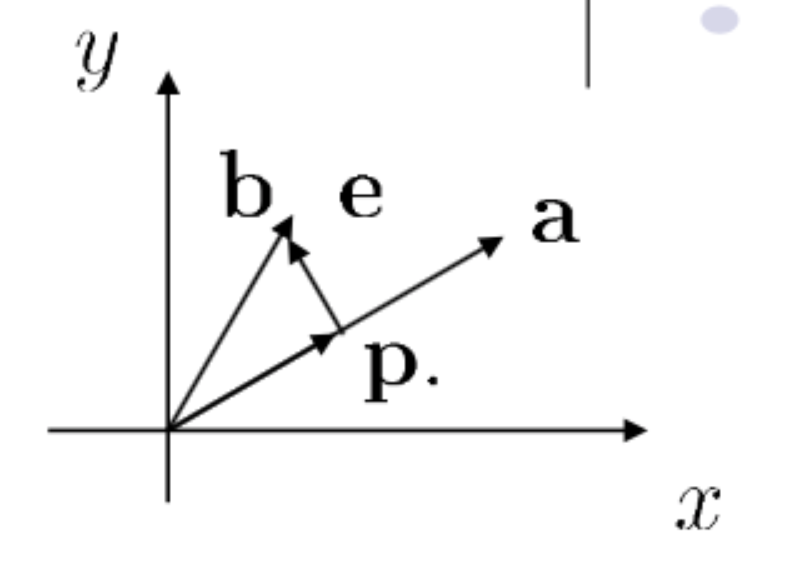
如图所示，求$b$在$a (a \neq 0)$上的投影向量$p$

$$\left\{\begin{array}{l}{p+e=b, e \perp \alpha} \\ {p=t \alpha(t \in R)}\end{array}\right.$$ $$\mathbf{e} \perp \mathbf{a} \Longrightarrow \mathbf{a}^{T}(\mathbf{b}-t \mathbf{a})=0 \Longrightarrow t=\frac{\mathbf{a}^{T} \mathbf{b}}{\mathbf{a}^{T} \mathbf{a}}(\mathbf{a} \neq \mathbf{0})$$

即$\mathbf{b}$在$\mathbf{a}$上的投影向量为$\left(\frac{\mathbf{a}^{T} \mathbf{b}}{\mathbf{a}^{T} \mathbf{a}}\right) \mathbf{a}=\mathbf{p}$

$$\left(\mathbf{a}^{T} \mathbf{b}\right) \mathbf{a}=\mathbf{a}\left(\mathbf{a}^{T} \mathbf{b}\right)=\left(\mathbf{a} \mathbf{a}^{T}\right) \mathbf{b}$$

因此，$\mathbf{p}=\left(\frac{\mathbf{a} \mathbf{a}^{T}}{\mathbf{a}^{T} \mathbf{a}}\right) \mathbf{b}$

其中$S=\frac{\mathbf{a} \mathbf{a}^{T}}{\mathbf{a}^{T} \mathbf{a}}$称为投影矩阵，$S$满足$S^{2}=S, S^{T}=S$
$\forall \mathbf{b} \in \mathbb{R}^{2}$，$S \mathbf{b}$是$\mathbf{b}$在$\mathbf{a}$上的投影向量

点在平面上的投影

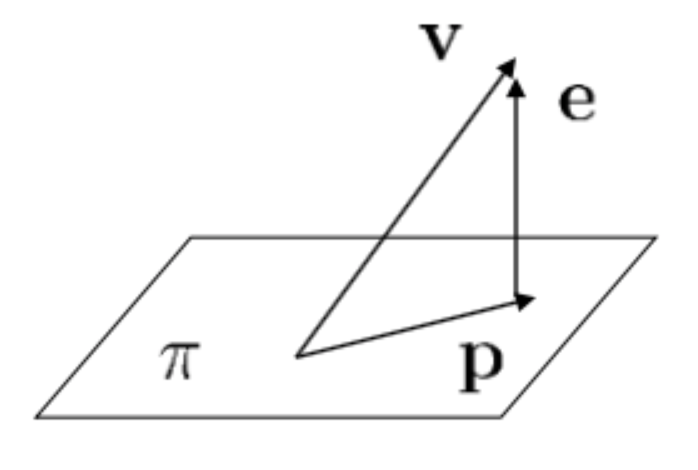
现在我们考虑点在平面上的投影。给定$\mathbf{v}=\left(v{1}, v{2}, v{3}\right)^{T} \in \mathbb{R}^{3}$，平面$\pi : a x+b y+c z=0$。设$\mathbf{P}$是$\mathbf{v}$在$\pi$上的投影，求$\mathbf{P}$。
令$\alpha{1}, \alpha{2}$是平面$\pi$上的两无关向量，即$a x+b y+c z=0$的基础解系或$N((a, b, c))$的一组基。
令$A=\left(\alpha{1}, \alpha{2}\right)$，则平面$\pi=C(A)$，求投影$\mathbf{p} \Longleftrightarrow$求$\mathbf{v}$关于$\mathbb{R}^{3}=C(A)+N\left(A^{T}\right)$的分解$\mathbf{v}{l}+\mathbf{v}{l n}$，其中$\mathbf{v}{l}=\mathbf{p}, \mathbf{v}_{l n}=\mathbf{e} \in N\left(A^{T}\right)$

$$\begin{array}{l}{\mathbf{p}=\mathbf{v}_{l} \in C(A) \Longleftrightarrow \exists \hat{\mathbf{x}}, A \hat{\mathbf{x}}=\mathbf{p}} \\ {\mathbf{e}=\mathbf{v}-\mathbf{p} \perp \pi \Longrightarrow A^{T}(A \hat{\mathbf{x}}-\mathbf{v})=\mathbf{0}}\end{array}$$

即$\hat{\mathbf{x}}$是$A^{T} A \mathbf{x}=A^{T} \mathbf{v}$的解。$A^{T} A$是可逆矩阵（A列满秩）$\Longrightarrow \hat{\mathbf{x}}=\left(A^{T} A\right)^{-1} A^{T} \mathbf{v}$，则$\mathbf{p}=A\left(A^{T} A\right)^{-1} A^{T} \mathbf{v}$。
此时，$A\left(A^{T} A\right)^{-1} A^{T}$为投影矩阵

一般地，一个矩阵$P$满足$P^{2}=P, P^{T}=P$，则称$P$为投影矩阵

定理：若$P$是一个投影矩阵，则$C(P)=N(I-P), N(P)=C(I-P)$
证明：从P(I-P)=(I-P)P=0思考

最小二乘法

回到解方程组$A{m \times n} \mathbf{x}=\mathbf{b}$
$A \mathbf{x}=\mathbf{b}$有解$\Longleftrightarrow \mathbf{b} \in C(A)$
假设它无解，则$\mathbf{b} \notin C(A)$，此时问题转化为：
求$\hat{\mathbf{x}}$使得$\Vert A \hat{\mathbf{x}}-\mathbf{b}\Vert$最小，即$\min {\mathbf{x} \in \mathbb{R}^{n}}\Vert A \hat{\mathbf{x}}-\mathbf{b}\Vert$的最小值点。
$\hat{\mathbf{x}}$为最小二乘解（the least square solution）
$A^{T} A \hat{\mathbf{x}}=A^{T} \mathbf{b}$称为法方程组（normal equations）

性质：
1.法方程组总有解（无论A是否列满秩），这是因为$C\left(A^{T}\right)=C\left(A^{T} A\right), A^{T} \mathbf{b} \in C\left(A^{T}\right)=C\left(A^{T} A\right)$
2.$A^{T} A \hat{\mathbf{x}}=A^{T} \mathbf{b}$的解可能有无穷个，但$A \hat{\mathbf{x}}$（投影p）唯一。
3.若A列满秩，则$A^{T} A$可逆，$\hat{\mathbf{x}}=\left(A^{T} A\right)^{-1} A^{T} \mathbf{b}$

最小二乘法的应用：曲线拟合

给定数据$\left{\left(x{1}, y{1}\right), \cdots,\left(x{N}, y{N}\right)\right}$
寻求直线$y=C+D x$，使得误差

$$E(C, D)=\left[y_{1}-\left(C+D x_{1}\right)\right]^{2}+\cdots+\left[y_{N}-\left(C+D x_{N}\right)\right]^{2}$$

最小，即使向量：

$$\left(\begin{array}{c}{y_{1}-\left(C+D x_{1}\right)} \\ {\vdots} \\ {y_{N}-\left(C+D x_{N}\right)}\end{array}\right)$$

的长度最小。
令

$$A=\left(\begin{array}{cc}{1} & {x_{1}} \\ {\vdots} & {\vdots} \\ {1} & {x_{N}}\end{array}\right), \mathbf{b}=\left(\begin{array}{c}{y_{1}} \\ {\vdots} \\ {y_{N}}\end{array}\right), \hat{\mathbf{x}}=\left(\begin{array}{c}{\hat{C}} \\ {\hat{D}}\end{array}\right)$$

即求$\hat{\mathbf{x}}$使得$\Vert A \hat{\mathbf{x}}-\mathbf{b}\Vert$最小。解法方程组$A^{T} A \hat{\mathbf{x}}=A^{T} \mathbf{b}$，即

$$\left(\begin{array}{cc}{N} & {\sum_{i=1}^{N} x_{i}} \\ {\sum_{i=1}^{N} x_{i}} & {\sum_{i=1}^{N} x_{i}^{2}}\end{array}\right)\left(\begin{array}{l}{\hat{C}} \\ {\hat{D}}\end{array}\right)=\left(\begin{array}{c}{\sum_{i=1}^{N} y_{i}} \\ {\sum_{i=1}^{N} x_{i} y_{i}}\end{array}\right)$$

令$\overline{x}=\frac{1}{N} \sum{i=1}^{N} x{i}, \overline{y}=\frac{1}{N} \sum{i=1}^{N} y{i}$，求得$\hat{C}=\overline{y}-\hat{D} \overline{x}, \hat{D}=\frac{x{1} y{1}+\cdots+x{N} y{N}-N \overline{x} \overline{y}}{x{1}^{2}+\cdots+x{N}^{2}-N \overline{x}^{2}}$
直线$y=\hat{C}+\hat{D} x$称为最小二乘直线。