参考资料:
清华大学数学科学系-线性代数-马辉
《工程数学 线性代数 第六版》 同济大学数学系 高等教育出版社
Linear Algebra by Gilbert Strang MIT麻省理工线性代数公开视频课
基和维数
$\left{\mathbf{v}{1}, \cdots, \mathbf{v}{n}\right}$是$V$的一个基(basis)
(1)$\mathbf{v}{1}, \cdots, \mathbf{v}{n}$线性无关
(2)$\forall \alpha \in V, \alpha$是$\mathbf{v}{1}, \cdots, \mathbf{v}{n}$的线性组合
我们说$V$的维数(dimension)是$n =$基中向量个数
定理:设$V$是一个向量空间,$\left{\mathbf{v}{1}, \cdots, \mathbf{v}{n}\right}$是一组基,$\left{\mathbf{w}{1}, \cdots, \mathbf{w}{m}\right}$是另一组基,则$m=n$
命题:$\mathbb{R}^{n}$中任意$n+1$个向量线性相关
性质:设$\mathbf{v}{1}, \cdots, \mathbf{v}{n}$是$\mathbb{R}^{n}$的一组基,$A$是一个$n \times n$可逆矩阵,则$A \mathbf{v}{1}, \cdots, A \mathbf{v}{n}$也是$\mathbb{R}^{n}$的一组基。
关于秩的不等式
(1) $r(A)=r\left(A^{T}\right)$
(2) $r(A B) \leq \min (r(A), r(B))$
(3) $r(A+B) \leq r(A)+r(B)$
四个基本子空间
设A是一个$m \times n$阶矩阵,考虑:
列空间(column space)$C(A)=\left{\mathbf{y} \in \mathbb{R}^{m} | \mathbf{y}=A \mathbf{x}, \exists \mathbf{x} \in \mathbb{R}^{n}\right}$ $dim = r$
行空间(row space)$C\left(A^{T}\right)=\left{\mathbf{y} \in \mathbb{R}^{n} | \mathbf{y}=A^{T} \mathbf{x}, \exists \mathbf{x} \in \mathbb{R}^{m}\right}$ $dim = r$
零空间(null space)$N(A)=\left{\mathbf{x} \in \mathbb{R}^{n} | A \mathbf{x}=\mathbf{0}\right}$ $dim = n-r$
左零空间(left null space)$N\left(A^{T}\right)=\left{\mathbf{x} \in \mathbb{R}^{m} | A^{T} \mathbf{x}=\mathbf{0}\right} =\left{\mathrm{x} \in \mathbb{R}^{m} | \mathrm{x}^{T} A=0\right}$ $dim = m-r$
维数公式
设$V$是一个向量空间,$W{1}, W{2}$是两个子空间,则$W{1} \cap W{2}$和$W{1}+W{2}$是$V$的子空间,但$W{1} \cup W{2}$一般不是子空间
这些空间的维数有如下关系:
$\operatorname{dim} W{1}+\operatorname{dim} W{2}=\operatorname{dim}\left(W{1} \cap W{2}\right)+\operatorname{dim}\left(W{1}+W{2}\right)$
四个子空间的正交性
定义:设$S$和$T$是$\mathbb{R}^{n}$的两个子空间(subspaces),我们说$S$垂直(perpendicular)于$T$,如果对于$\forall \mathbf{v} \in S, \mathbf{w} \in T, \mathbf{v}^{T} \mathbf{w}=0$,记作$S \perp T$或$T \perp S$。我们也可以说:$S$和$T$是正交(orthogonal)的。
定理:设$A$是$m \times n$阶矩阵,则$C(A)$和$N\left(A^{T}\right)$正交,$C\left(A^{T}\right)$和$N(A)$正交。
四个子空间还有如下的关系:
$C\left(A^{T}\right)+N(A)=\mathbb{R}^{n}, C\left(A^{T}\right) \perp N(A)$
$C(A)+N\left(A^{T}\right)=\mathbb{R}^{m}, C(A) \perp N\left(A^{T}\right)$
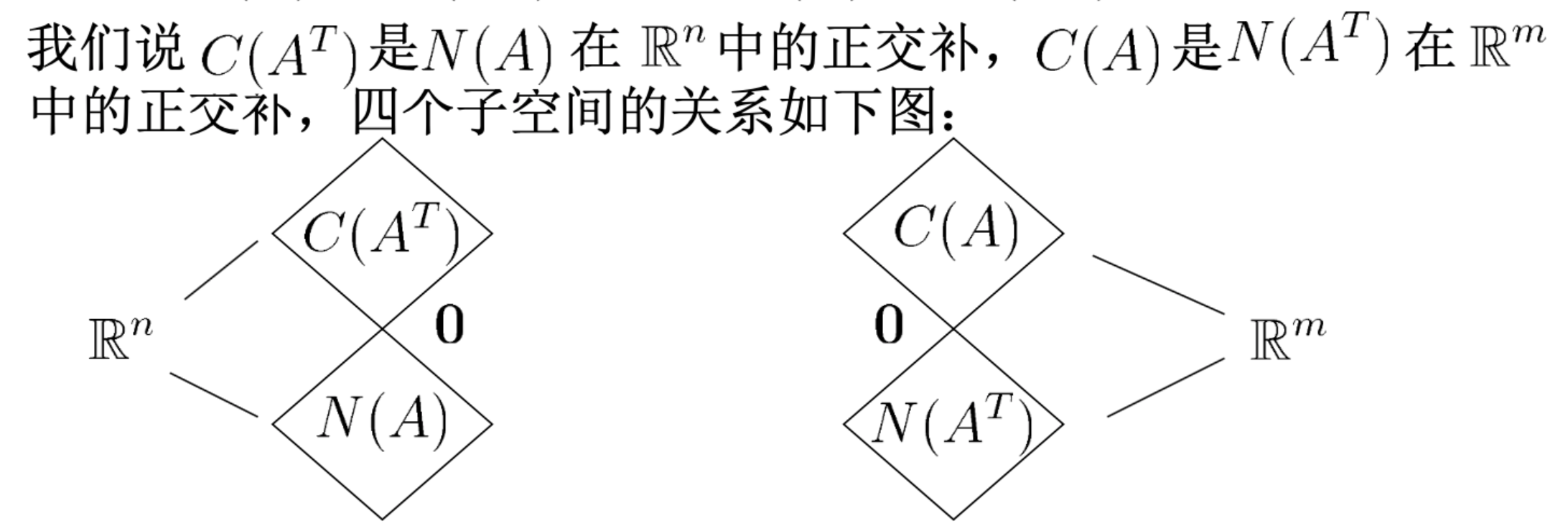
正交补定义:设$V \subset \mathbb{R}^{n}$是一个子空间,$V$在$\mathbb{R}^{n}$中的正交补定义为集合$\left{\mathbf{w} \in \mathbb{R}^{n} | \mathbf{v}^{T} \mathbf{w}=0, \forall \mathbf{v} \in V\right}$,记作$V^{\perp}$
Ax=b在行空间中的唯一性
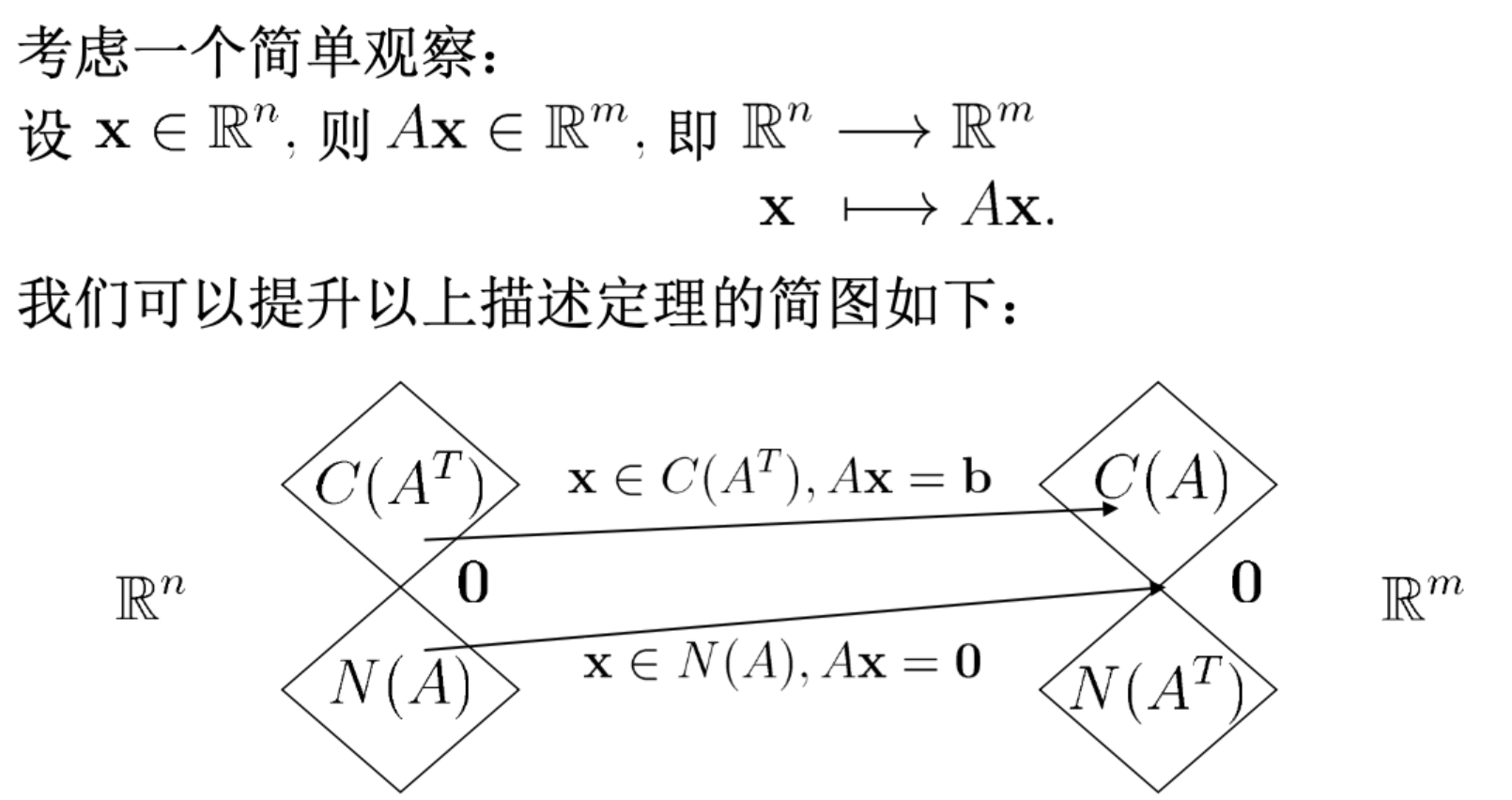
定理:若$A \mathbf{x}=\mathbf{b}$有解,则$A \mathbf{x}=\mathbf{b}$在$C\left(A^{T}\right)$中有唯一解