复习线性代数: 矩阵与线性方程组
参考资料:
清华大学数学科学系-线性代数-马辉
《工程数学 线性代数 第六版》 同济大学数学系 高等教育出版社
Linear Algebra by Gilbert Strang 麻省理工视频公开课程
2.1 矩阵与向量的乘积
矩阵与向量乘积以旋转变换为例:
矩阵$
\left(
\begin{matrix}
\cos \varphi&-\sin \varphi\
\sin \varphi&\cos \varphi\
\end{matrix}
\right)
$对应的线性变换
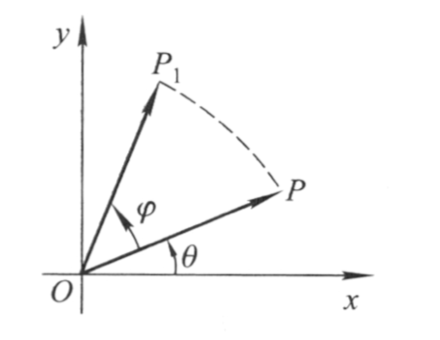
把$xOy$平面上的向量$\overrightarrow{O P}=(x,y)$变换为向量$\overrightarrow{O P{1}}=(x{1},y_{1})$。
设$\overrightarrow{OP}$的长度为$r$,辐角为$\theta$,即设$x=r \cos \theta, y=r \sin \theta$,那么
表明$\overrightarrow{O P_{1}}$的长度为$r$,而辐角为$\theta+\varphi$。因此,这是把向量$\overrightarrow{OP}$(依逆时针方向)旋转$\varphi$角(即把点P以原点为中心逆时针旋转$\varphi$角)的旋转变换。
进一步还可推知,用
,相当于把向量$\overrightarrow{O P}$按逆时针方向旋转n个$\varphi$角,即旋转$n \varphi$角,而旋转$n\varphi$角的变换所对应的矩阵为
,亦即成立
2.2 可逆矩阵
若对于方阵$A$: $A \mathbf{x}=\mathbf{b}$对任意向量$\vec b$有唯一解,则矩阵$A$是可逆的(invertible)。可逆矩阵的列向量线性无关(linearly independent),且$A \mathbf{x}=\mathbf{0}$只有零解。不可逆矩阵称为奇异(singular)矩阵,列向量是线性相关的(linearly depentent),$A \mathbf{x}=\mathbf{0}$有无穷多解。
2.3 线性方程组的行图和列图
方程组的行图(row picture)
例子1:给定线性方程组
它可以写成矩阵的形式
从行(row)的角度看,每行代表一条直线,方程组的解为两直线的交点
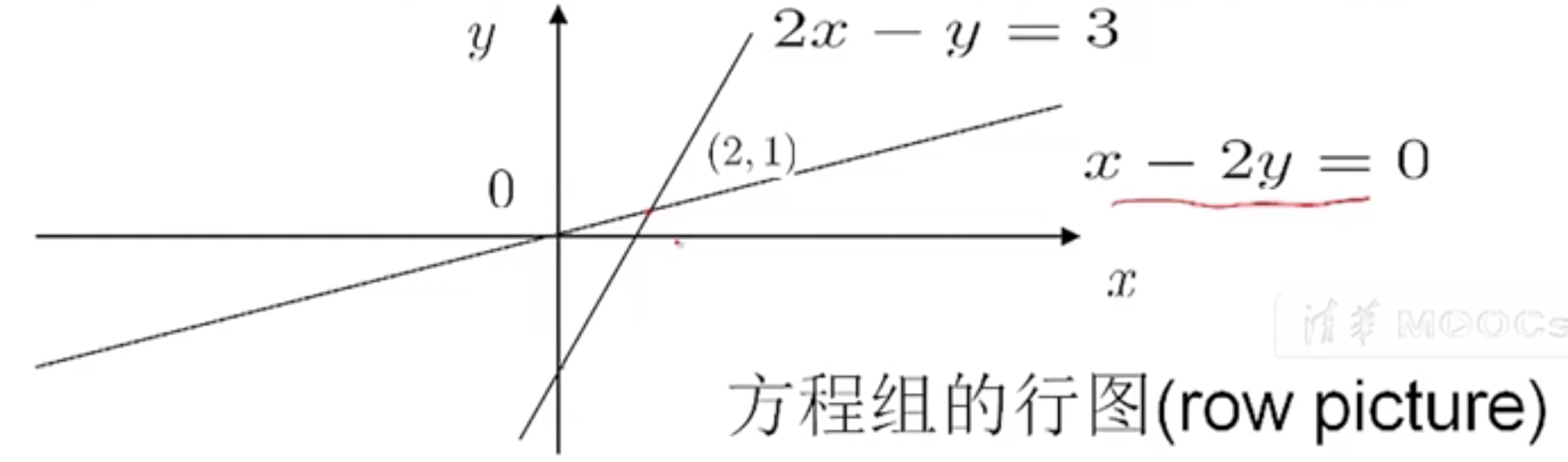
方程组的列图(column picture)

例2:
行图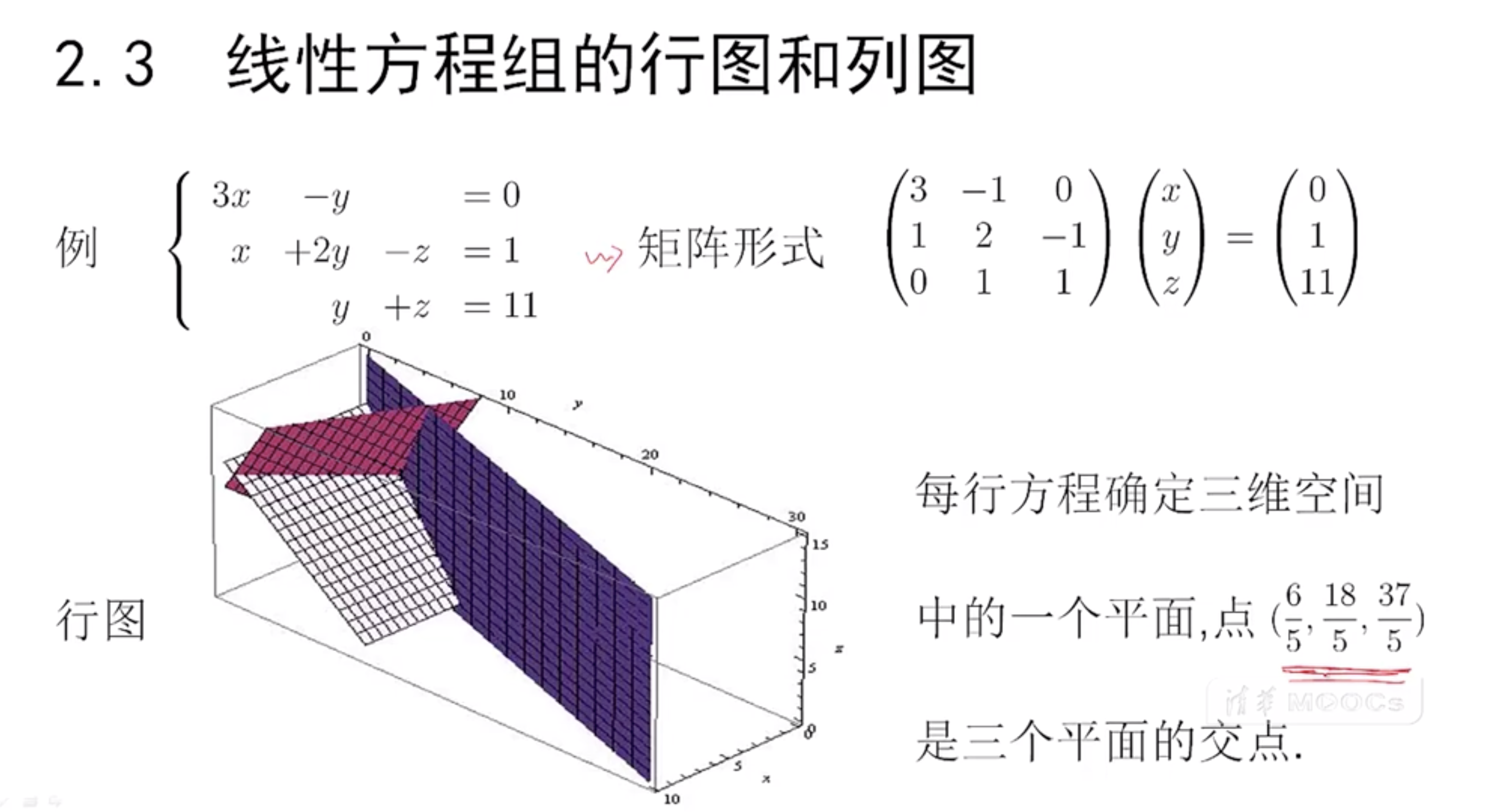
列图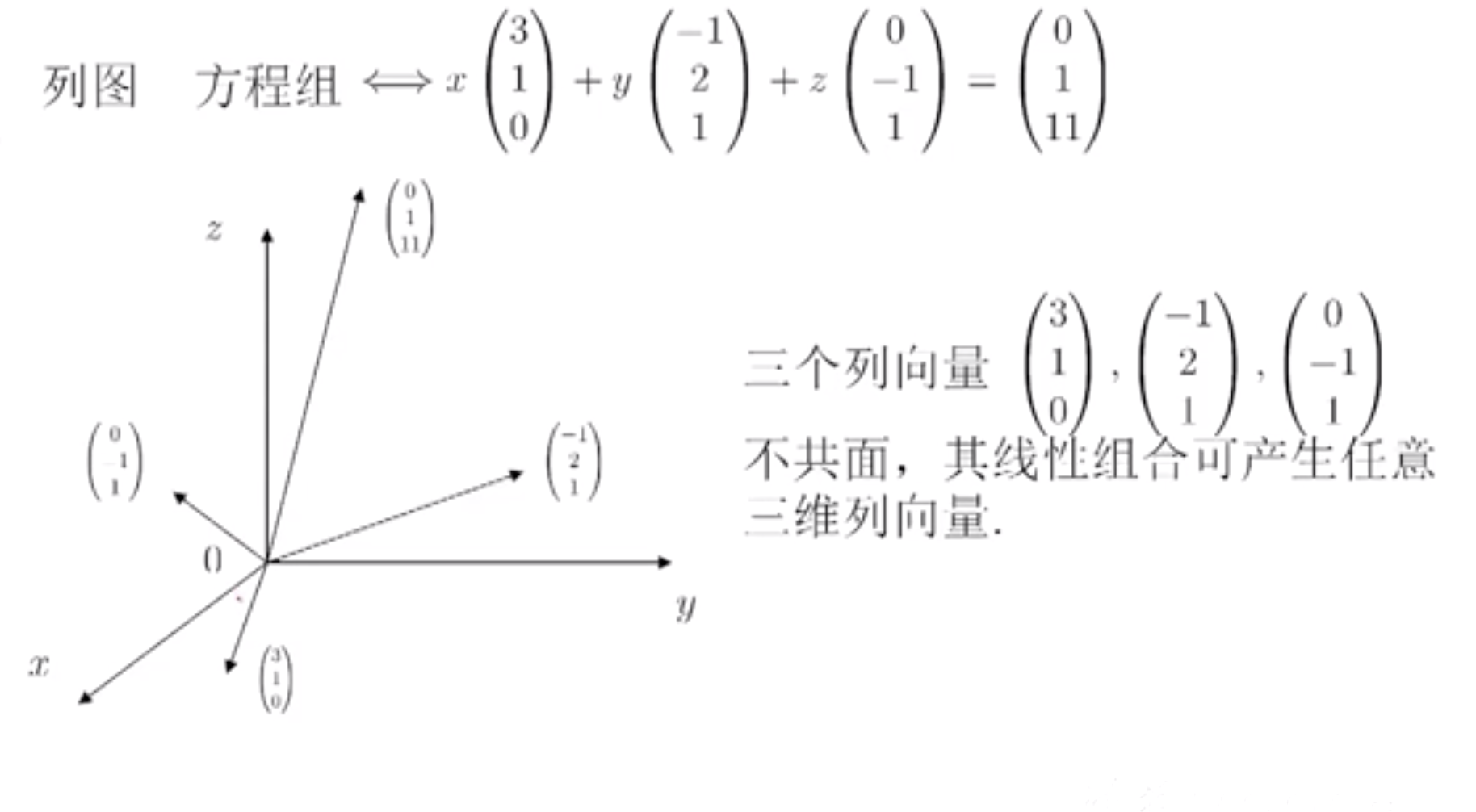
从行图,列图去理解方程组有唯一解,无解和无穷多解
唯一解的行图列图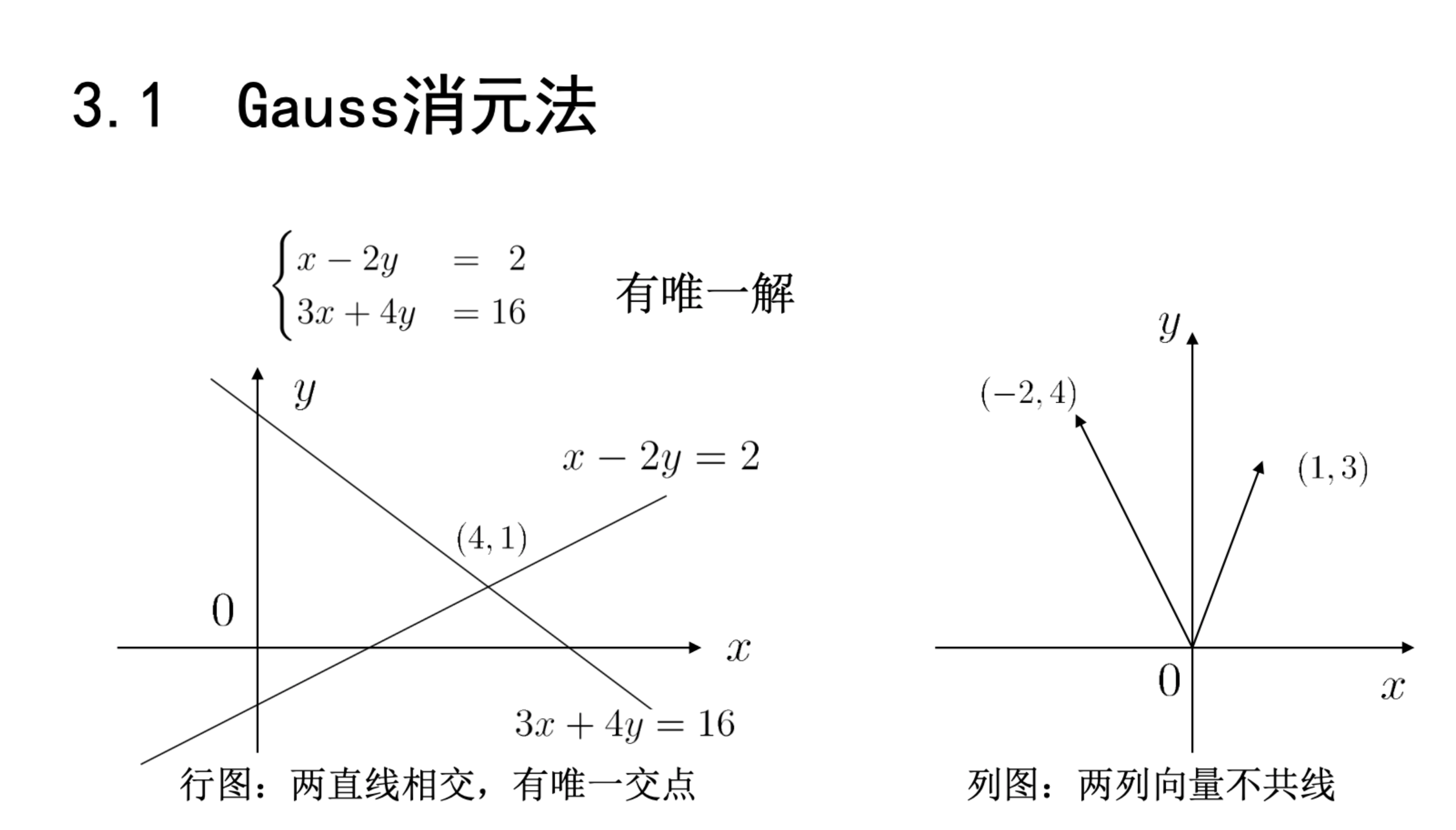
无解的行图列图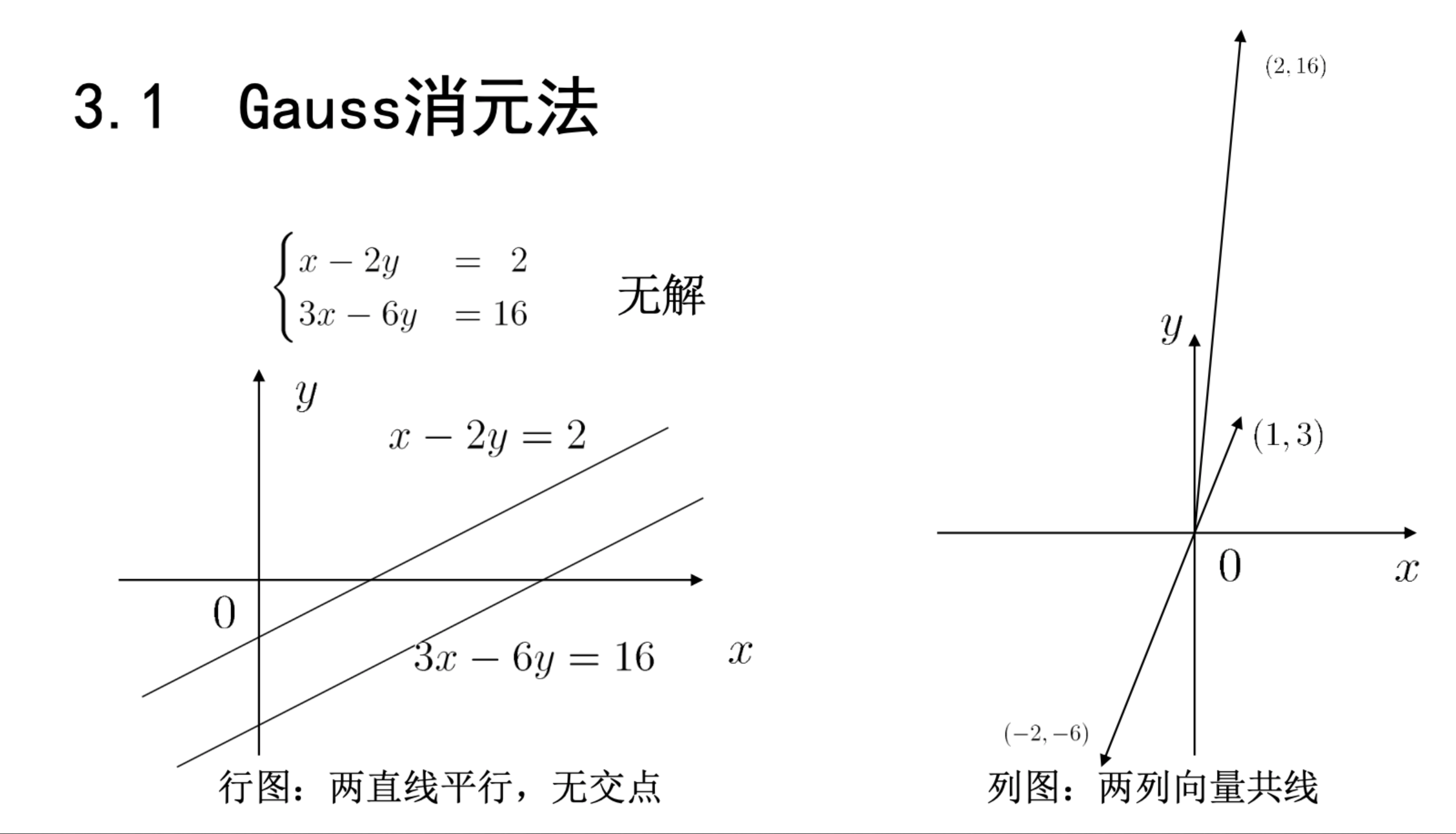
无穷多解的行图列图